«Двогорба Росія»: дискусія про аналіз статистики по виборам до Держдуми
Наше деловое партнерство www.banwar.org
Від редакції: Ми публікуємо відгук експерта на статтю «Двогорба Росія» і коментар автора. 
Владислав СУХОВОЛЬСЬКИЙ, докт. біол. наук, професор, Федеральний дослідний центр РАН, Красноярськ В № 214 газети «Троїцький Варіант - Наука» від 4 жовтня 2016 була опублікована стаття експерта Сергія Шпількіна, в якій аналізуються підсумки минулих виборів до Державної Думи РФ і затверджується, що в ході цих виборів мали місце значні фальсифікації на користь однієї з брали участь у виборах партій [1].
Мені видається, що я маю право прокоментувати цю статтю і її висновки. Справа в тому, що я та людина, яка в 1990 році придумав ті методи статистичного аналізу результатів голосувань, які зараз використовуються для виявлення фальсифікацій. Г-н Шпількин, перераховуючи роботи по темі статистичного аналізу результатів голосувань, регулярно починає їх з нашої монографії (Собянін А. А., СУХОВОЛЬСЬКИЙ В. Г. Демократія, обмежена фальсифікаціями. М .: Проектна група з прав людини, 1995). Другий у списку пана Шпількіна зазвичай йде монографія американських політологів, один з авторів якої М. Мягков - наш колишній співробітник.
Якщо пан Шпількин читав нашу монографію (а наскільки я знаю, він робив це), то він повинен був знати, що використаний в його статті тест на явку - лише один з цілого набору статистичних тестів на фальсифікації, запропонований нами. Цей тест необхідний, але недостатній для твердження про існування фальсифікацій. І для точного і достовірного висновку про наявність фальсифікації бажано перевірити дані голосування з використанням ВСІХ можливих тестів.
Ще один простий тест на фальсифікації для країни з досить однорідним електоратом полягає в аналізі зв'язку логарифма числа тих, хто голосував за партію або кандидата і логарифма місця, зайнятого цією партією (кандидатом). Якщо все чесно, то зв'язок між цими величинами описується прямою лінією. Хочу навести кілька прикладів з практики голосувань в різних країнах в останні роки (рис. 1-3).
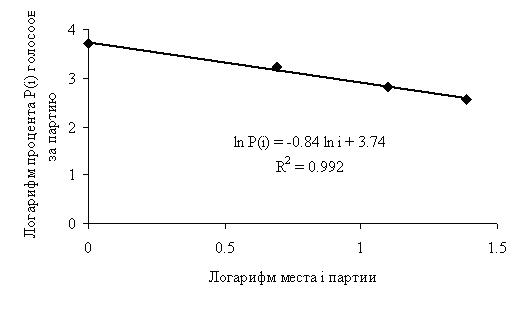
Мал. 1. Парламентські вибори в Туреччині в 2015 році  Мал. 2. Парламентські вибори у Фінляндії в 2015 році
Мал. 2. Парламентські вибори у Фінляндії в 2015 році 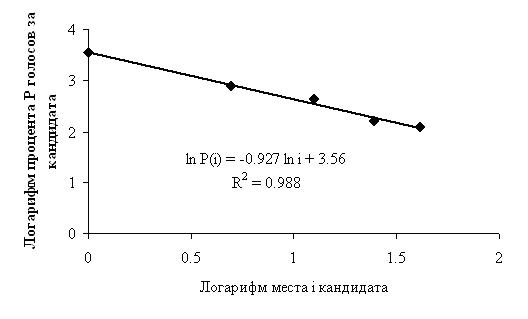 Мал. 3. Праймеріз в Нью-Гемпширі (штат з досить етнічно однорідним населенням) в 2016 році Як видно, з країнами, де ніхто не кричить про фальсифікації, все нормально: і рангове розподіл голосів за партії або кандидатів лінійно в подвійних логарифмічних координатах, і коефіцієнт детермінації R2 дуже близький до одиниці (прошу вибачення за статистичний жаргон, але я сподіваюся, що читачі «Троїцького варіанту» ці речі знають). Якщо ж мали місце фальсифікації, то умова лінійності не виконується і точки, що характеризують політичну партію (кандидата), на користь яких відбувалися фальсифікації, будуть «відскакувати» від прямої, а коефіцієнт детермінації буде зменшуватися.
Мал. 3. Праймеріз в Нью-Гемпширі (штат з досить етнічно однорідним населенням) в 2016 році Як видно, з країнами, де ніхто не кричить про фальсифікації, все нормально: і рангове розподіл голосів за партії або кандидатів лінійно в подвійних логарифмічних координатах, і коефіцієнт детермінації R2 дуже близький до одиниці (прошу вибачення за статистичний жаргон, але я сподіваюся, що читачі «Троїцького варіанту» ці речі знають). Якщо ж мали місце фальсифікації, то умова лінійності не виконується і точки, що характеризують політичну партію (кандидата), на користь яких відбувалися фальсифікації, будуть «відскакувати» від прямої, а коефіцієнт детермінації буде зменшуватися.
Як же виглядає рангове розподіл голосів, поданих за все партії, що брали участь у виборах 2016? На рис. 4 і 5 наведені ці розподілу, побудовані за офіційними даними ЦВК і за даними гіпотези пана Шпількіна.
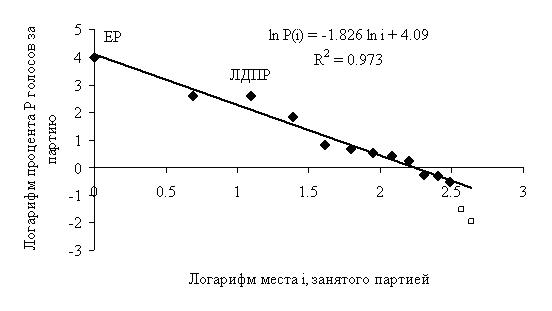
Мал. 4. Розподіл голосів на виборах в Державну Думу РФ в 2016 році (офіційні дані) 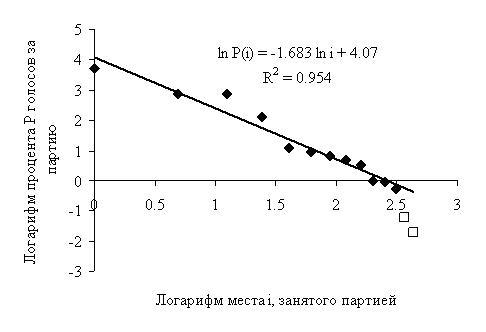 Мал. 5. Розподіл голосів на виборах в Державну Думу РФ в 2016 році (гіпотеза С. Шпількіна) Як видно з рис. 4, лише одна точка - дані по ЛДПР (третє місце) - «відскакує» від теоретичної прямої. Зауважимо, що в разі фальсифікацій на користь «ЕР» точка, що характеризує її результати, повинна була лежати істотно ВИЩЕ теоретичної прямої. Якщо ж відкинути дані для ЛДПР, то для розподілу по іншим даними коефіцієнт детермінації R2 складе 0,983 (тобто практично 1!).
Мал. 5. Розподіл голосів на виборах в Державну Думу РФ в 2016 році (гіпотеза С. Шпількіна) Як видно з рис. 4, лише одна точка - дані по ЛДПР (третє місце) - «відскакує» від теоретичної прямої. Зауважимо, що в разі фальсифікацій на користь «ЕР» точка, що характеризує її результати, повинна була лежати істотно ВИЩЕ теоретичної прямої. Якщо ж відкинути дані для ЛДПР, то для розподілу по іншим даними коефіцієнт детермінації R2 складе 0,983 (тобто практично 1!).
Розподіл же, побудоване на основі гіпотези пана Шпількіна, істотно гірше описується теоретичною моделлю. Більш того, з цього графіка випливає, що фальсифікації проводилися проти (!) «ЕР». Ну вже в це я не вірю (я думаю, і всі нормальні люди теж). Друге пояснення спостережуваного виду розподілу на рис. 5 - щось не так з гіпотезою С. Шпількіна.
Що ж трапилося, в чому причина спостережуваних відхилень? У масовій фальсифікації за ЛДПР? Можна розглянути різні гіпотези, що пояснюють відхилення на рис. 4 без використання гіпотези про наявність фальсифікацій. Але, напевно, газета не найкраще місце для складних статистичних викладок.
Хочеться сказати тільки одне. У медичній етиці є одне зовні дуже просте правило для лікарів: «Не нашкодь!» Йдеться про те, що лікар не завжди може допомогти хворому, але він зобов'язаний проводити лікування так, щоб хворому не стало гірше. Звісно ж, що таке ж правило повинно стати нормою для людей, що займаються кількісної політологією. Мені видається, що тільки після детального аналізу результатів голосувань на всіх рівнях (федеральному, регіональному, територіальному і т. П.) Можна виступати з коректними висновками (ми свого часу аналізували навіть на рівні окремих виборчих дільниць, а їх в РФ близько 100 тис .!). І ще: потрібно розуміти, що всі виборці голосували одночасно і на виборах по федеральному списку, і на виборах в одномандатних округах, і при масових фальсифікаціях результатів виборів за партійними списками потрібно одночасно фальсифікувати і результати виборів по одномандатних округах - інакше не зійдеться явка на тих та інших виборах. Значить, потрібно перевіряти всі результати. Зрозуміло, за пару днів і навіть за пару тижнів такий аналіз не виконати - це копітка і дуже занудотна робота. Але вона необхідна. В іншому випадку, якщо глобальні висновки робляться на основі довільно обраного критерію, виборців «залікують» і вони будуть думати, що всі вибори в нашій країні завжди фальсифікуються. А це, по всій видимості, далеко не так - приведу лише один приклад (рис. 6).
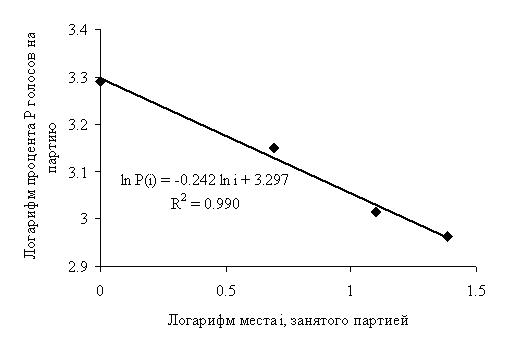
Мал. 6. Результати виборів в Державну Думу РФ в 2011 році по Владивостоку (КПРФ - 26,86%, «ЕР» - 23,32%, «СР» - 20,42%, ЛДПР - 19,37%) Я зовсім не стверджую , що ніяких фальсифікацій на минулих (і попередніх) виборах не було. Цілком можливо, що вони були, і навіть багато. Але я абсолютно точно впевнений в тому, що глобальні висновки про наявність фальсифікацій не можна робити на основі одного простого тесту. Потрібно все ж поважати науку, якій ти займаєшся.
- Сергій Шпількин. Двогорба Росія // ТРВ-Наука. № 214 від 4 жовтня 2016 року. http://trv-science.ru/2016/10/04/dvugorbaya-rossiya/
Редакція попросила Сергія Шпількіна прокоментувати відгук Владислава СУХОВОЛЬСЬКИЙ.

Сергій Шпількин, незалежний дослідник виборів Книга А.А.Собяніна і В.Г.Суховольского (далі «С-С») «Демократія, обмежена фальсифікаціями: вибори і референдуми в Росії в 1991-1993 роках», видана в 1995 році [1 ], - важлива фундаментальна праця, що поклала початок дослідженням статистики виборів в Росії. Деякі з підходів, запропонованих в цій книзі, залишаються актуальними і донині. Наприклад, «діаграма Собяніна - СУХОВОЛЬСЬКИЙ», т. Е. Діаграма розсіювання для результатів кандидатів по ділянках в координатах «явка - результат кандидата» (початково у С-С "явка - частка тих, хто проголосував за кандидата від усіх зареєстрованих виборців») залишається одним з найнаочніших і простих способів оцінити загальну ситуацію з голосуванням в країні в цілому або в окремому регіоні. У певному сенсі я навіть радий, що не був знайомий з цією книгою в 2007 році, коли мене зацікавили результати виборів до Державної Думи, - інакше я, швидше за все, не став би заглиблюватися в дані до рівня ділянок, визнавши, що все цікаве вже зрозуміле і знайдено. Зрозуміло, ця книга не може не займати одне з перших місць в будь-якому списку літератури з статистичному аналізу виборів. Тому я дуже радий, що один з авторів цієї книги В.Г.Суховольскій відгукнувся на мою замітку в ТРВ-Наука № 214, написану за підсумками думських виборів 18 вересня. Однак з тезами, висловленими в цьому відгуку, я, на жаль, погодитися не можу.
В.Г.Суховольскій дорікає мене в тому, що я нехтую запропонованим в його з А.А.Собяніним книзі критерієм «чесності» виборів, що передбачає наявність лінійної залежності між логарифмом відсотка голосів за кандидата і логарифмом місця, зайнятого цим кандидатом (= рангу кандидата в ранжируваному спаданням результатів списку). Згідно С-С, ця «... чисельна закономірність носить загальний характер і описує ситуацію" вільної конкурентної боротьби "за розподіл кінцевого кількості будь-яких умовних" благ "» (глава 7). По суті, як відзначають С-С, ця закономірність є окремим випадком т.зв. закону Ціпфа - Парето. При цьому автори заявляють, що «виконання рівняння (1) для виборчого процесу означає, що існує" вільна конкуренція "всіх кандидатів, що мають можливість безперешкодно пояснити свої політичні погляди і політичну платформу виборцям».
І сам описаний вище критерій, і висновки, які на його підставі робить в своєму відгуку В.Г.Суховольскій, видаються мені сумнівними. По-перше, критерій не витримує чисто технічної «перевірки на вошивість»: він з великою ймовірністю не виконується в ситуації, коли кандидати, які посіли на виборах перше і друге місця, показують близькі результати. За прикладом далеко ходити не треба: візьмемо перший тур виборів президента Франції в 2012 році (тоді перше місце з результатом 28,63% зайняв Франсуа Олланд, а друге з результатом 27,18% - Ніколя Саркозі). Як легко бачити, залежність дуже далека від передбачуваної лінійної.
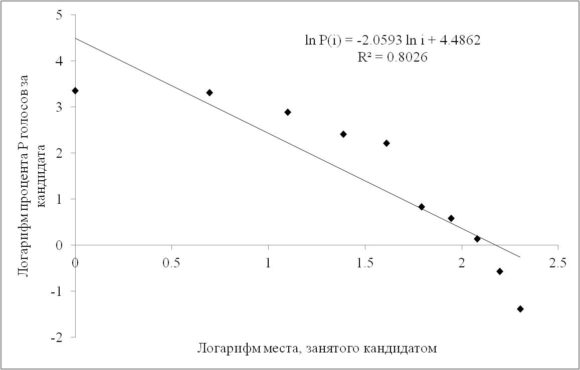
Мал. 1. Перший тур президентських виборів у Франції (2012) По-друге, згідно з С-С, сам критерій ґрунтується на припущенні про вільну конкуренцію всіх кандидатів в інформаційному просторі. Якщо це припущення можна було прийняти в якості «нульового наближення» в перші роки виборів в Російській Федерації (досить згадати, що на виборах 1993 року до Державної Думи проурядовий блок «Вибір Росії» програв ЛДПР, посівши друге місце), то вважати нинішню ситуацію в Росії вільною конкуренцією кандидатів з рівним доступом до інформаційних ресурсів більш ніж дивно.
По-третє, як справедливо зазначає В.Г.Суховольскій, «глобальні висновки про наявність (додам від себе - і відсутності) фальсифікацій не можна робити на основі одного простого тесту». Дійсно, наявність фальсифікацій на виборах в Росії було неодноразово продемонстровано в численних аналізах, заснованих на набагато більш докладних даних, ніж результати голосування за кандидатів по країні в цілому, - см., Наприклад, [2, 3, 4, 5, 6, 7 ], і аналіз, наведений у моїй замітці, треба розглядати в цьому контексті.
І останнє зауваження загального характеру, що відноситься не тільки до цієї дискусії, а й до інших апеляцій до «закону Ціпфа». Воно стосується використання коефіцієнта детермінації R2 як показника якості регресії. Дивлячись на ефектні значення R2 на графіках в відкликання В.Г.Суховольского, треба пам'ятати, що в нормі при регресії в якості «нульової гіпотези» передбачається, що пояснюється змінна незалежна від пояснює. Однак це не так в нашому випадку, коли яка пояснюється змінна - це результат партії, а пояснює - її номер в ранжируваному списку. Якщо взяти ряд випадкових числових значень і впорядкувати його по спадаючій (або зростання), номер величини в упорядкованому ряду (ранг) буде, очевидно, коррелирован з її значенням. Наприклад, як показано в [7], ряди (a1 ... an) і (rank a1 ... rank an), де a1 ... an - значення нормально розподіленої випадкової величини, при 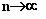 корельовані з
корельовані з 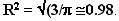 . Оскільки логарифм рангу, в свою чергу, коррелирован з рангом, а логарифм величини - з величиною, то, навіть якщо ми візьмемо для результатів партій (a1 ... an) просто випадкові значення, ми «задарма» отримаємо деяку ненульову величину R2 для залежності між результатом партії і логарифмом його рангу. Більш того, при вдалому виборі типу випадкової величини ця «дармова» частина може бути дуже суттєвою. Як показує чисельний експеримент, якщо взяти в якості ai величини, зворотні рівномірно розподіленим в інтервалі (0, 1) випадкової величини, і n = 12 (кількість партій, що враховуються В.Г.Суховольскім на його графіках для думських виборів 2016 року, - дві останні в рейтингу він чомусь виключає з розгляду), то ймовірність отримати для рядів (ln rank a1 ... rank ln an) і (ln a1 ... ln an) коефіцієнт детермінації R2> 0,97 (як на рис. 4 у В. Г.Суховольского) для випадково вибраних таким чином «результатів партій» становить 15% (оскільки всі числа стоять під логу рими, піклуватися про приведення суми «результатів» до 100% не потрібно). На мій погляд, це ще один привід задуматися про те, чи є кореляція логарифма результатів кандидатів з логарифмом зайнятого місцем скільки-небудь змістовним фактом.
. Оскільки логарифм рангу, в свою чергу, коррелирован з рангом, а логарифм величини - з величиною, то, навіть якщо ми візьмемо для результатів партій (a1 ... an) просто випадкові значення, ми «задарма» отримаємо деяку ненульову величину R2 для залежності між результатом партії і логарифмом його рангу. Більш того, при вдалому виборі типу випадкової величини ця «дармова» частина може бути дуже суттєвою. Як показує чисельний експеримент, якщо взяти в якості ai величини, зворотні рівномірно розподіленим в інтервалі (0, 1) випадкової величини, і n = 12 (кількість партій, що враховуються В.Г.Суховольскім на його графіках для думських виборів 2016 року, - дві останні в рейтингу він чомусь виключає з розгляду), то ймовірність отримати для рядів (ln rank a1 ... rank ln an) і (ln a1 ... ln an) коефіцієнт детермінації R2> 0,97 (як на рис. 4 у В. Г.Суховольского) для випадково вибраних таким чином «результатів партій» становить 15% (оскільки всі числа стоять під логу рими, піклуватися про приведення суми «результатів» до 100% не потрібно). На мій погляд, це ще один привід задуматися про те, чи є кореляція логарифма результатів кандидатів з логарифмом зайнятого місцем скільки-небудь змістовним фактом.
література
- Собянін А.А., СУХОВОЛЬСЬКИЙ В.Г. Демократія, обмежена фальсифікаціями. М .: Проектна група з прав людини, 1995. http://hrights.ru/text/sob/
- Kobak D., Shpilkin S., and Pshenichnikov MS Integer percentages as electoral falsification fingerprints // Ann. Appl. Stat. 2016. 10 (1). P. 54-73. https://arxiv.org/abs/1410.6059
- Kobak D., Shpilkin S., and Pshenichnikov MS Statistical anomalies in 2011-2012 // Russian elections revealed by 2D correlation analysis. 2012. arXiv: 1205.0741v2. https://arxiv.org/abs/1205.0741
- Enikolopov R., Korovkin V., Petrova M., Sonin K., Zakharov A. Field experiment estimate of electoral fraud in Russian parliamentary elections // Proceedings of the National Academy of Sciences 110 (2). P. 448-452. http://www.pnas.org/content/110/2/448.full
- С.В. Мухлеж на виборах: перевірка за дві секунди // ТРВ-Наука. № 141 від 5 листопада 2013 року. http://trv-science.ru/2013/11/05/mukhljozh-na-vyborakh-proverka-v-dva-scheta/
- С.В. Про арифметику і трошки про вибори // ТРВ-Наука. № 99 від 13 березня 2012 року. http://trv-science.ru/2012/03/13/pro-arifmetiku-i-nemnozhko-pro-vybory/
- Овчинников Б. 18 чесних міст // ТРВ-Наука. № 98 від 28 лютого 2012 року. http://trv-science.ru/2012/02/28/sto-vosemdesyat-chestnykh-gorodov/
- Stuart A. The correlation between variate-values and ranks in samples from a continuous distribution // British Journal of Mathematical and Statistical Psychology. 1954. 7 (1). P. 37-44.
Якщо ви знайшли помилку, будь ласка, виділіть фрагмент тексту і натисніть Ctrl + Enter.
пов'язані статті
Як же виглядає рангове розподіл голосів, поданих за все партії, що брали участь у виборах 2016?Що ж трапилося, в чому причина спостережуваних відхилень?
У масовій фальсифікації за ЛДПР?