1. Вступ У статті розглядається один з підходів до визначення корисного сигналу (тенденції) потокових...
2. Основна проблема
3. кластерний фільтр
4. Порядок побудови кластерних фільтрів
5. Приклад простого кластерного фільтра
6. Програмний код і результат роботи кластерного фільтра
7. Ефект випереджаючого згладжування
8. ефект кобри
9. Помилки, що випереджають тенденцію
10. імпульсна характеристика
11. ідеальний фільтр
12. Висновок

Вступ

Наше деловое партнерство www.banwar.org

У статті розглядається один з підходів до визначення корисного сигналу (тенденції) потокових даних. Невеликі практичні тести фільтрації (згладжування) біржових котирувань демонструють потенційну можливість створення цифрових фільтрів (індикаторів), що не запізнюються за часом і не перемальовувати на останніх барах.

звичайний підхід

Цей підхід заснований на класичних методах згладжування часових рядів. Про це є безліч статей, як на цьому ресурсі, так і на інших. Результати отримуємо теж класичні:

1. Зміна тенденції проявляється з запізненням;
2. За збільшення реакції індикатора (цифрового фільтра) доводиться платити зниженням якості згладжування;
3. Спроби реалізації не запізнілих індикаторів призводять до їх перемальовуванні на останніх отсчетах (барах).

Якщо трейдери навчилися з цим боротися, використовуючи інерційність економічних процесів і інші хитрощі, то при оцінці експериментальних даних в реальному часі, наприклад при випробуванні авіаційних конструкцій, це неприйнятно.

Основна проблема

Не секрет, що більшість торгових систем з плином часу перестають працювати. Або те, що індикатори тільки на деяких ділянках показові. Пояснення цьому просте: ринкові котирування нестаціонарні. Просте визначення стаціонарності процесу є в Вікіпедії :

Стационарность - властивість процесу не міняти свої характеристики згодом. Має сенс в декількох розділах науки.

Судячи з визначення, методи аналізу стаціонарних часових рядів не мають сенсу в технічному аналізі. Воно і зрозуміло, як тільки ми порахуємо характеристики відомого ряду біржових котирувань, в ринок увійде хитрий маркетмейкер і зробить наші розрахунки безглуздими.

Незважаючи на очевидність цього факту, величезна кількість індикаторів будуються на основі теорії аналізу стаціонарних часових рядів. Прикладом таких індикаторів є ковзаючі середні і їх модифікації. Є, правда, спроби створення адаптивних індикаторів. Ніби як вони повинні в тій чи іншій мірі враховувати нестаціонарність біржових котирувань, але щось дива не відбувається. Спроби "покарати" маркетмейкера, використовуючи відомі на сьогодні методи аналізу нестаціонарних рядів ( вейвлети , емпіричні моди та інші), теж не приводять до успіху. Схоже на те, що не береться якийсь ключовий фактор.

Основна причина такого стану справ полягає в тому, що використовувані методи не призначені для роботи з потоковими даними. Всі вони (або майже все) розроблялися для аналізу вже відомих даних або, в термінології технічного аналізу, історичних даних. Ці способи зручні, наприклад, в геофізики: "струснув" землю, отримав сейсмограму і потім пару місяців її вивчаєш. Тобто вони прийнятні там, де виникають при фільтрації невизначеності на кінцях часового ряду несуттєво впливають на кінцевий результат.

При аналізі експериментальних потокових даних або біржових котирувань максимальний інтерес представляє не історія, а останні дані, що надійшли. Саме ті дані, з якими не вміють працювати класичні алгоритми.

кластерний фільтр

Кластерний фільтр (англ. Cluster - гроно, згусток, пучок) - сукупність цифрових фільтрів, аппроксимирующих вихідну послідовність. Кластерний фільтр не варто плутати з кластерними індикаторами .

Кластерний фільтр зручно використовувати для аналізу нестаціонарних часових рядів в реальному часі, іншими словами - потокових даних. Це означає, що найбільший інтерес такий фільтр, наприклад, не для згладжування вже відомих значень часового ряду, а для отримання найбільш ймовірного згладженого значення нового даного, отриманого в реальному часі.

На відміну від всіляких методів декомпозиції (розкладання на складові) або просто фільтрів потрібної частоти, кластерні фільтри створюють композицію або віяло можливих значень вихідного ряду, які в подальшому піддаються додатковому аналізу для апроксимації вихідної послідовності. Вхідна послідовність більше грає роль орієнтиру, ніж те, що аналізують. Основному аналізу піддають значення, пораховані набором фільтрів після опрацювання надходження даного.

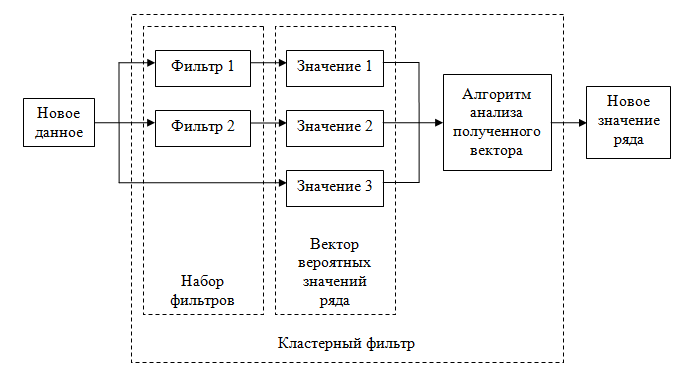
Малюнок 1. Схема простого кластерного фільтра

У загальному випадку кожен фільтр, включений в кластер, володіє своїми індивідуальними характеристиками і ніяк не пов'язаний з іншими. Іноді ці фільтри налаштовані для аналізу нікого свого стаціонарного часового ряду, який описує окремі властивості вихідного нестаціонарного. У найпростішому випадку, якщо вихідний нестаціонарний ряд змінює свої параметри, то відбувається "перемикання" між фільтрами. Таким чином, кластерний фільтр відстежує зміну характеристик в реальному часі.

Порядок побудови кластерних фільтрів

Будь-кластерний фільтр може бути створений в три етапи:

1. Найчастіше перший етап найскладніший, але саме на цьому етапі формуються імовірнісні моделі одержуваних потокових даних. Цих моделей може бути як завгодно багато. Вони не завжди мають відношення до фізичних процесів, які впливають на функції, що апроксимується дані. Чим точніше моделі описують апроксимується послідовність, тим більша ймовірність одержати не запізнюється за часом кластерний фільтр.

2. На другому етапі під кожну модель створюється один або кілька цифрових фільтрів. Саме загальне умова об'єднання фільтрів в кластер є те, що вони належать моделям, що описують апроксимується послідовність.

3. Отже, ми можемо мати від одного і більше фільтрів в кластері. Відповідно, на кожному новому відліку у нас є величина самого відліку і одне або більше значень фільтрів. Таким чином, на кожному відліку у нас є вектор або штучний шум з декількох значень (мінімум два). Все, що тепер потрібно зробити, так це вибрати найбільш підходяще значення.

Приклад простого кластерного фільтра

Для прикладу реалізуємо простий кластерний фільтр, відповідний схемою, зображеної на малюнку 1. В якості вхідної послідовності візьмемо котирування. Можна взяти просто ціни закриття будь-якого таймфрейма.

1. Опис прийнятої моделі. Будемо виходити з таких припущень:

• Апроксимується послідовність нестаціонарна, тобто має властивість змінювати свої характеристики з плином часу.
• Ціна закриття бару не є дійсною ціною бару. Тобто зафіксована ціна закриття бару є одним з шумових рухів, як і інші рухи ціни на цьому барі.
• Дійсна ціна або дійсне значення аппроксимируемой послідовності знаходиться між ціною закриття поточного бару і ціною закриття попереднього бару.
• Апроксимується послідовність прагне зберігати свій напрямок. Тобто, якщо на попередньому барі вона росла, то на поточному барі вона прагне зберегти зростання.

2. Підбираємо цифрові фільтри. Для простоти візьмемо два фільтри:

• Перший фільтр у нас буде просте ковзне середнє ( Simple Moving Average ), Що розраховується за останніми двома цінами закриття. На мій погляд, це добре вписується в третю умову нашої моделі.
• Так як процес у нас нестаціонарний, то спробуємо ввести додатковий фільтр в надії, що це якось допоможе вловити зміни характеристик часового ряду. З видом розумного шамана я вибрав експоненціальне ковзне середнє ( Exponential Moving Average ). Вибрав тільки через те, що EMA швидше MA і не повинна давати запізнювання на тренді і краще реагує на шум. EMA теж будемо розраховувати за останніми двома цінами закриття.

3. Вибираємо найбільш підходяще значення для кластерного фільтра.

Отже, на кожному новому відліку будемо мати значення самого відліку (ціна закриття), значення MA і EMA. Ціну закриття будемо ігнорувати, виходячи з другого умови нашої моделі. Далі вибираємо значення МА або ЕМА, виходячи з останнього умови моделі, тобто з умови проходження тренду:

• Для зростаючого тренду, тобто CF (i-1)> CF (i-2), вибираємо один з наступних чотирьох варіантів:

  якщо CF (i-1) <MA (i) і CF (i-1) <EMA (i), то CF (i) = MIN (MA (i), EMA (i));

  якщо CF (i-1) <MA (i) і CF (i-1)> EMA (i), то CF (i) = MA (i);

  якщо CF (i-1)> MA (i) і CF (i-1) <EMA (i), то CF (i) = EMA (i);

  якщо CF (i-1)> MA (i) і CF (i-1)> EMA (i), то CF (i) = MAX (MA (i), EMA (i)).

• Для спадного тренда, тобто CF (i-1) <CF (i-2), вибираємо один з наступних чотирьох варіантів:

  якщо CF (i-1)> MA (i) і CF (i-1)> EMA (i), то CF (i) = MAX (MA (i), EMA (i));

  якщо CF (i-1)> MA (i) і CF (i-1) <EMA (i), то CF (i) = MA (i);

  якщо CF (i-1) <MA (i) і CF (i-1)> EMA (i), то CF (i) = EMA (i);

  якщо CF (i-1) <MA (i) і CF (i-1) <EMA (i), то CF (i) = MIN (MA (i), EMA (i)).

тут:

• CF (i) - значення кластерного фільтра на поточному барі;
• CF (i-1) і CF (i-2) - значення кластерного фільтра на попередніх барах;
• MA (i) - значення простий ковзної середньої на поточному барі;
• EMA (i) - значення експоненційної ковзної середньої на поточному барі;
• MIN - мінімальне значення;
• MAX - максимальне значення;

Програмний код і результат роботи кластерного фільтра

Код індикатора з нашим кластерним фільтром не складніше коду змінного середнього. Тому тут його розбирати не має сенсу, там немає якогось ноу-хау. Исходник прикладений до статті.

Не гаючи часу, приклад роботи нашого індикатора можна подивитися на відео:

Відео 1. Результат роботи простого кластерного фільтра

Незважаючи на те, що створення фільтра було схоже на легке чаклунство, ніж на строгий математичний підхід, на відео добре помітно, що лінія кластерного фільтра поводиться адекватніше окремо взятих ковзають середніх. Особливо це видно на пилкоподібних ділянках вихідного ряду. Якщо когось не вразило, то ще, наприклад, можна порівняти з JJMA, який вважається одним з кращих індикаторів. На наступному відео ту саму ділянку, але на ньому змагаються JJMA і наш фільтр. Параметри JJMA постарався підібрати так, щоб його лінія по максимуму збігалася з нашим індикатором.

Відео 2. Порівняння простого кластерного фільтра і JJMA

В середньому, наш фільтр не програє JJMA на будь-яких таймсеріях. Але якщо з JJMA вже не отримати щось краще, то наш кластерний фільтр можна поліпшити.

Ефект випереджаючого згладжування

До сих пір не було жодного підтвердження, що кластерні фільтри здатні згладжувати вихідну послідовність без запізнення. Для досягнення подібного результату потрібне створення більш складного фільтра, ніж той, який ми розглянули вище.

Для демонстрації був зроблений індикатор GMomentum test . Він містить дві індикаторних лінії:

• Синя - класичний моментум.
• Червона - класичний моментум, згладжений кластерним цифровим фільтром, в якому реалізований більш складний алгоритм.

В налаштуваннях індикатора є різні варіанти тестів, які спеціально підготовлені для статті. В описаних нижче тестах використовується відносний моментум як у Вільяма Блау . Для своїх експериментів можете використовувати інші варіації Моментум, результати будуть такими ж. Детальний опис, інструкції з встановлення і використання індикатора знайдете в описі самого індикатора.

Якогось особливого аргументу на користь вибору Momentum для статті у мене немає, просто лінія Моментум досить сильно зашумлена і тому робота фільтра, на мій погляд, найбільш показова. Загалом, запускаєте індикатор GMomentum test і вивчаєте, як веде себе червона лінія в порівнянні з синьою.

Для початку розглянемо один цікавий момент. Для цього при запуску індикатора необхідно встановити параметр "Filter" в "Test No.1 Advance". В цьому режимі настройки фільтра такі, що досить часто проявляється ефект, який можна назвати випереджаючим. При тестуванні ви не побачите згладжування всієї вихідної лінії Моментум. Фільтр вишукує ділянки, де є ймовірність отримати випереджаюче ефект. Тож не дивно, що це виходить не завжди. Але досить часто, щоб можна було це помітити.

На графіку нижче представлений один з показових ділянок роботи фільтра.

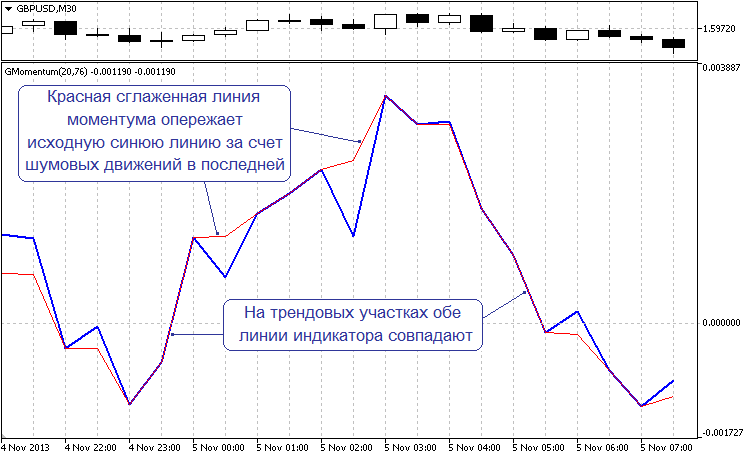
Малюнок 2. Випереджальне ефект при згладжуванні лінії Моментум

Варто відзначити, що це тільки видимість випереджаючої фільтрації. Ця видимість виникає виключно через присутніх шумових рухів самої лінії Моментум, а не тому, що фільтр випередив час. Подібні дослідження інших індикаторів (від простого MA до JJMA) підтверджують, що ефект випереджаючого згладжування можна спостерігати на кожному з них. І чим менше встановлений період, тим частіше це проявляється. Останні напрацювання показують, що ефект можна підсилити. Все залежить тільки від способу формування вектора можливих значень і його аналізу.

ефект кобри

Той, хто вже бачив індикатор в роботі, міг звернути увагу ще на одну аномалію. Лінія індикатора на останньому незавершеному барі не завжди слід за ціною. Наприклад, ціна може зростати, а індикатор рухається вниз. І навпаки. При швидкому ринку або в візуалізаторі це часом нагадує язичок кобри, яким вона намацує шлях до видобутку.

Відео 3. Випереджаючий згладжування і ефект кобри

Помилки, що випереджають тенденцію

Вище було показано, що коли вихідна лінія Моментум помиляється (шумить) проти тенденції, то це призводить до ефекту випередження вихідної лінії згладженої лінією. Очевидно, що лінія Моментум може помилятися і в іншу сторону, тобто несподівано проскочити далеко в напрямку тенденції, і навіть непристойно довго затримуватися там, хоча тренд вже розвернувся. Буде логічним, якщо фільтр почне пригальмовувати такі рухи.

Давайте подивимося, як працює алгоритм при фільтрації ось таких випереджальних тенденцію помилок. Для цього при запуску індикатора необхідно встановити параметр "Filter" в "Test No.2 Smoothing". Робота кластерного фільтра під час цього тесту розділена на дві частини.

У короткому імені індикатора "GMomentum (Параметр 1, Параметр 2)", який відображається в подокне графіка, в дужках є два параметри. Якщо другий параметр дорівнює -1, то відбувається спроба виправити (згладити) помилки, що випереджають тенденцію. Якщо другий параметр дорівнює або вище нуля, то підключаються настройки для отримання випереджаючого згладжування.

На відео нижче можна побачити роботу фільтра при зміні його чутливості від мінімуму до прийнятного значення і назад. В індикаторі для управління чутливістю (при активному вікні індикатора) натискайте клавіші Up і Down, щоб домогтися подібного ефекту як на відео.

Відео 4. Фільтрація помилок, які випереджають тенденцію.

На відео зверху видно, що, незважаючи на різкі рухи ціни і вихідної лінії Моментум, згладжування лінії Моментум при збільшенні чутливості фільтра відбувається без затримки. При максимальному згладжуванні отримуємо прийнятні точки входу.

До речі, флетовій ділянки є бідою більшості індикаторів. Тут же, навіть при цих налаштуваннях, деякі з них легко вироджуються майже в пряму лінію. Теоретично, використовуючи цю методику, можна поліпшити будь-який з існуючих індикаторів без створення додаткового запізнювання. Практично - потрібно перевіряти.

На наступному відео зверніть увагу на те, що фільтр "з'їдає" сильні піки вихідної лінії Моментум і практично без запізнювання отрісовиваєт тенденцію, яка, до слова, близька до руху ціни і більш гладка. Пояснення, чому це так, є в статті про індикатори Вільяма Блау .

Відео 5. Згладжування піків вихідної лінії Моментум.

Отриманий результат не на всій історії котирувань такий вражаючий. Але з огляду на той факт, що моментум володіє великими шумовими рухами і те, що індикатор робився всього-на-всього для демонстрації фільтрації потокових даних без затримки по часу, можна вважати його цілком прийнятним. На додаток варто відзначити, що індикатор перемальовується.

імпульсна характеристика

Дослідження характеристик Моментум з вбудованим фільтром можуть виявитися вельми цікавими. Наприклад, імпульсна характеристика добре демонструє, як і куди зникають піки на лінії індикатора. Для тесту необхідно встановити параметр "Filter" в "Test No.3 Impulse". Під час тесту на кожному 1 024 барі подається одиничний імпульс. Після старту індикатора знайдіть цей момент на графіку. Він повинен виглядати так:

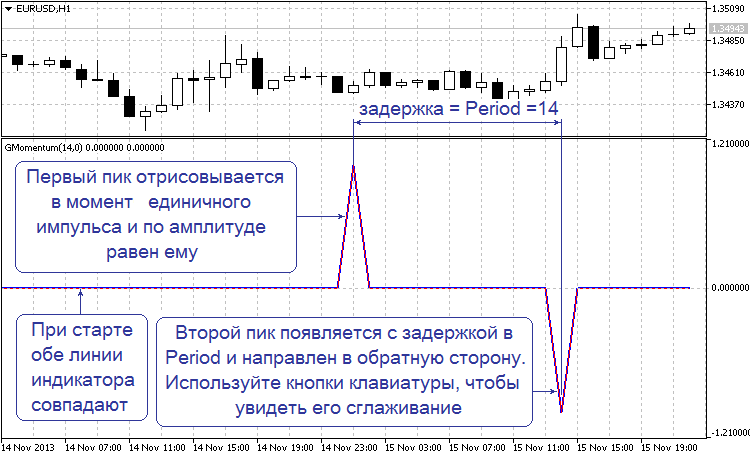
Малюнок 3. Імпульсна характеристика Моментум

При запуску індикатора фільтр відключений. Тому ви побачите два піки на синьою і червоною лінії. Один пік буде в момент одиничного імпульсу і дорівнює йому, інший - спрямований у протилежний бік через вказану кількість періодів. Саме так виглядає імпульсна характеристика "голого" Моментум. Далі, за допомогою клавіш Up і Down поступово збільшуйте або зменшуйте чутливість фільтра. У вас повинно вийти щось подібне:

Відео 6. Імпульсна характеристика Моментум

Як бачите, фільтр поступово під корінь "з'їдає" другий пік і абсолютно не чіпає перший. Фільтр повністю виправляє те, що накоїв моментум і в точності відтворює вихідну картину: одиничний імпульс в чистому полі. Немає ніякого запізнювання. Ні спотворення амплітуди одиничного імпульсу і його форми. Що це? Робота ідеального фільтра?

ідеальний фільтр

Є один суттєвий фактор, який не дозволяє відразу вважати розглянутий фільтр ідеальним. Але про це трохи нижче.

Існує фіксована ідея, що ідеального фільтра не може бути. Що всі фільтри (індикатори) запізнюються. Тоді як пояснити отримані результати? Всі вони представлені як то, що можна спостерігати. Хитра робота програміста? Мабуть, можна схитрувати в коді з одиничним імпульсом. Але ж це все проявляється на будь-яких котируваннях. При цьому немає необхідності якось налаштовувати або перенастроювати індикатор під кожен торговий інструмент.

Коли ми будуємо фільтр з фізичних об'єктів (конденсатор, індуктивність і т.п.), ідеального фільтра не може бути. Про це добре подбала сама природа. Але коли ми маємо справу з цифровим світом, то хіба побудова ідеального фільтра не можливо? Природно, що відповідь потрібно давати, нехтуючи фізичними обмеженнями обчислювальних систем (точність, швидкість розрахунку і т.п.).

Повернемося до нашого індикатору. Вбудований цифровий фільтр не відноситься до лінійних. І те, що вище названо імпульсною характеристикою, для індикатора з вбудованим фільтром просто вдалий окремий випадок фільтрації. Для того щоб робити будь-які далекосяжні висновки, потрібно провести більш коректне і ретельне дослідження.

Висновок

Сподіваюся, що матеріал, поданий у статті, зруйнує деякі стереотипи щодо побудови цифрових фільтрів (індикаторів).

Все, що описано, можна досліджувати за допомогою запропонованих індикаторів. Представлена ​​версія GMomentum test дозволить всім оцінити працездатність і потенційні можливості кластерних фільтрів. А простий приклад фільтра може підштовхнути розробників на створення своїх.

На завершення, візьму на себе сміливість зробити наступний висновок: створення повноцінних чи не запізнюється за часом індикаторів (цифрових фільтрів) потенційно можливо.