1. Вступ
2. 1. Розподілу, сутність, види
3. 2. Теоретичні розподілу ймовірностей
4. 3. Створення графіків розподілів
5. Висновок

Наше деловое партнерство www.banwar.org

Вся теорія ймовірності грунтується на практиці небажаність.
(Леонід Сухоруков)

Вступ

За родом своєї діяльності трейдер змушений дуже часто стикатися з такими категоріями, як ймовірність і випадковість. На іншому полюсі щодо випадковості знаходиться таке поняття, як "закономірність". Дивно, але в силу загальфілософських законів, випадковість, як правило, переростає в закономірність. Про зворотному поки говорити не будемо. Загалом, співвідношення випадковість-закономірність є ключовим, тому що воно, в контексті ринку, безпосередньо впливає на розмір отримуваної трейдером прибутку.

У даній статті я спробую розповісти про теоретичні базових інструментах, які в подальшому допоможуть знаходити деякі ринкові закономірності.

1. Розподілу, сутність, види

Отже, для опису деякої випадкової величини нам буде потрібно одномірне статистичне розподіл ймовірностей . Воно буде описувати деяку вибірку випадкових величин за певним законом, тобто, щоб застосувати будь-якої закон розподілу, нам буде потрібно якийсь безліч випадкових величин.

Навіщо нам аналізувати [теоретичні] розподілу? З їх допомогою нескладно виявляти закономірності зміни частот в залежності від значень варьирующего ознаки. Крім того, можна отримати деякі статистичні параметри потрібного розподілу.

Що стосується видів імовірнісних розподілів, то в спеціалізованій літературі найчастіше прийнято розділяти сімейство розподілів на безперервні і дискретні, в залежності від типу безлічі випадкових величин. Однак, існують і інші класифікації, наприклад, за такими критеріями, як: симетричність кривої розподілу f (x) відносно прямої x = x 0, параметр зсуву, кількість мод, інтервал випадкової величини та ін.

Є кілька способів, що дозволяють задати нам закон розподілу. Серед них потрібно відзначити найбільш популярні:

2. Теоретичні розподілу ймовірностей

Отже, давайте в рамках MQL 5 спробуємо створити класи, що описують статистичні розподілу. Крім того, я хотів додати, що в спеціалізованій літературі є багато прикладів коду, написаного на С ++, який можна успішно застосувати для MQL 5 кодування. Загалом, я не став винаходити колесо, в деяких випадках користувався напрацюваннями С ++ коду.

Найбільша складність, з якою зіткнувся, полягала у відсутності множинного спадкоємства в MQL5. Тому складні класові ієрархії використовувати не вдалося. Найоптимальнішим джерелом в плані С ++ коду стала книга Numerical Recipes: The Art of Scientific Computing [2], звідки було запозичене мною більшість функцій. Найчастіше, їх доводилося допрацьовувати під потреби MQL5.

2.1.1 Нормальний розподіл

Традиційно, почнемо з нормального розподілу .

Малюнок 1. Щільність нормального розподілу Nor (0,1)

Воно має наступну нотацію: X ~ Nor (μ, σ 2), де:

• X - це випадкова величина, обрана з нормального розподілу Nor;
• μ - параметр середнього (-∞ ≤ μ ≤ + ∞);
  
• σ - параметр дисперсії (0 <σ).
  

Допустимий діапазон випадкової величини X: -∞ ≤ X ≤ + ∞.

Формули, використані в статті, можуть відрізнятися від аналогічних з інших джерел. Іноді така різниця математично не принципово. У деяких випадках воно обумовлено різною параметризацією.

Нормальний розподіл грає велику роль в статистиці, тому що воно відображає закономірність, яка виникає при взаємодії безлічі випадкових причин, жодна з яких не має переважаючого впливу. І хоча нормальний розподіл - це велика рідкість на фінансових ринках, проте, важливо порівнювати з ним емпіричні розподілу для з'ясування заходи і характеру відхилення їх від нормального.

Визначимо клас CNormaldist для нормального розподілу наступним чином:

class CNormaldist: CErf {public: double mu, sig; void CNormaldist () {mu = 0,0; sig = 1.0; if (sig <= 0.) Alert ( "bad sig in Normal Distribution!"); } Double pdf (double x) {return (0.398942280401432678 / sig) * exp (- 0.5 * pow ((x-mu) / sig, 2)); } Double cdf (double x) {return 0.5 * erfc (- 0.707106781186547524 * (x-mu) / sig); } Double invcdf (double p) {if (! (P> 0. && p <1.)) Alert ( "bad p in Normal Distribution!"); return - 1.41421356237309505 * sig * inverfc (2. * p) + mu; } Double sf (double x) {return 1 -cdf (x); }};

Як можна помітити, клас CNormaldist є похідним класом від базового класу С Erf, який визначає в свою чергу клас функції помилок. Він нам знадобиться при розрахунку деяких методів класу CNormaldist. Сам клас С Erf і допоміжна функція erfcc виглядають приблизно так:

class CErf {public: int ncof; double cof [28]; void CErf () {int Ncof = 28; double Cof [28] = {- 1.3026537197817094, 6.4196979235649026 e- 1, 1.9476473204185836 e- 2, - 9.561514786808631 e- 3, - 9.46595344482036 e- 4, 3.66839497852761 e- 4, 4.2523324806907 e- 5, - 2.0278578112534 e- 5, - 1.624290004647 e- 6, 1.303655835580 e- 6, 1.5626441722 e- 8, - 8.5238095915 e- 8, 6.529054439 e- 9, 5.059343495 e- 9, - 9.91364156 e- 10, - 2.27365122 e- 10, 9.6467911 e- 11, 2.394038 e- 12, - 6.886027 e- 12, 8.94487 e- 13, 3.13092 e- 13, - 1.12708 e- 13, 3.81 e- 16, 7.106 e- 15, - 1.523 e- 15, - 9.4 e- 17, 1.21 e- 16 , - 2.8 e- 17}; setCErf (Ncof, Cof); }; void setCErf (int Ncof, double & Cof []) {ncof = Ncof; ArrayCopy (cof, Cof); }; void ~ CErf () {}; double erf (double x) {if (x> = 0.0) return 1.0 -erfccheb (x); else return erfccheb (-x) - 1.0; } Double erfc (double x) {if (x> = 0.0) return erfccheb (x); else return 2.0 -erfccheb (-x); } Double erfccheb (double z) {int j; double t, ty, tmp, d = 0.0, dd = 0,0; if (z <0) Alert ( "erfccheb requires nonnegative argument!"); t = 2.0 / (2.0 + z); ty = 4.0 * t- 2.0; for (j = ncof- 1; j> 0; j--) {tmp = d; d = ty * d-dd + cof [j]; dd = tmp; } Return t * exp (-z * z + 0.5 * (cof [0] + ty * d) -dd); } Double inverfc (double p) {double x, err, t, pp; if (p> = 2.0) return - 100.0; if (p <= 0.0) return 100.0; pp = (p <1.0)? p: 2.0 -p; t = sqrt (- 2. * log (pp / 2.0)); x = - 0.70711 * ((2.30753 + t * 0.27061) / (1.0 + t * (0.99229 + t * 0.04481)) - t); for (int j = 0; j <2; j ++) {err = erfc (x) -pp; x + = err / (M_2_SQRTPI * exp (- pow (x, 2)) - x * err); } Return (p <1.0? X: -x); } Double inverf (double p) {return inverfc (1.0 -p);}}; double erfcc (const double x) {double t, z = fabs (x), ans; t = 2 ./ (2.0 + z); ans = t * exp (-z * z- 1.26551223 + t * (1.00002368 + t * (0.37409196 + t * (0.09678418 + t * (- 0.18628806 + t * (0.27886807 + t * (- 1.13520398 + t * (1.48851587 + t * (- 0.82215223 + t * 0.17087277))))))))); return (x> = 0.0? ans: 2.0 -ans); }

2.1.2 логнормальний розподіл

Тепер давайте розглянемо логнормальний розподіл .

Малюнок 2. Щільність логнормального розподілу Logn (0,1)

Воно має наступну нотацію: X ~ Logn (μ, σ 2), де:

• X - це випадкова величина, обрана з логнормального розподілу Logn;
• μ - параметр зсуву (0 <μ);
  
• σ - масштабний параметр (0 <σ).
  

Допустимий діапазон випадкової величини X: 0 ≤ X ≤ + ∞.

Створимо клас CLognormaldist, що описує логнормальний розподіл . Він буде представлений таким чином:

class CLognormaldist: CErf {public: double mu, sig; void CLognormaldist () {mu = 0,0; sig = 1.0; if (sig <= 0.) Alert ( "bad sig in Lognormal Distribution!"); } Double pdf (double x) {if (x <0.) Alert ( "bad x in Lognormal Distribution!"); if (x == 0.) return 0.; return (0.398942280401432678 / (sig * x)) * exp (- 0.5 * pow ((log (x) -mu) / sig, 2)); } Double cdf (double x) {if (x <0.) Alert ( "bad x in Lognormal Distribution!"); if (x == 0.) return 0.; return 0.5 * erfc (- 0.707106781186547524 * (log (x) -mu) / sig); } Double invcdf (double p) {if (! (P> 0. && p <1.)) Alert ( "bad p in Lognormal Distribution!"); return exp (- 1.41421356237309505 * sig * inverfc (2. * p) + mu); } Double sf (double x) {return 1 -cdf (x); }};

Як можна помітити, логнормальний розподіл мало чим відрізняється від нормального. Різниця в тому, що параметр x замінений на log (x).

2.1.3 Розподіл Коші

розподіл Коші має наступну нотацію: X ~ Cau (μ, σ), де:

• X - це випадкова величина, обрана з розподілу Коші Cau;
• μ - параметр зсуву (-∞ ≤ μ ≤ + ∞);
  
• σ - масштабний параметр (0 <σ).
  

Допустимий діапазон випадкової величини X: -∞ ≤ X ≤ + ∞.

Малюнок 3. Щільність розподілу Коші Cau (0,1)

У MQL5 форматі, створене за допомогою класу CCauchydist, воно виглядає таким чином:

class CCauchydist {public: double mu, sig; void CCauchydist () {mu = 0,0; sig = 1.0; if (sig <= 0.) Alert ( "bad sig in Cauchy Distribution!"); } Double pdf (double x) {return 0.318309886183790671 / (sig * (1. + pow ((x-mu) / sig, 2))); } Double cdf (double x) {return 0.5 +0.318309886183790671 * atan2 (x-mu, sig); } Double invcdf (double p) {if (! (P> 0. && p <1.)) Alert ( "bad p in Cauchy Distribution!"); return mu + sig * tan (M_PI * (p- 0.5)); } Double sf (double x) {return 1 -cdf (x); }};

Тут потрібно відзначити, що використовується функція atan2 (), яка повертає головне значення арктангенса, виражене в радіанах:

double atan2 (double y, double x) {double a; if (fabs (x)> fabs (y)) a = atan (y / x); else {a = atan (x / y); if (a <0.) a = - 1. * M_PI_2 -a; else a = M_PI_2 -a; } If (x <0.) {if (y <0) a = a- M_PI; else a = a + M_PI; } Return a; }

2.1.4 Г іперболіческое секанс розподіл

Гіперболічне секанс розподіл зацікавить тих, хто аналізує фінансові ряди.

Малюнок 4. Щільність г іперболіческого секанс розподілу HS (0,1)

Воно має наступну нотацію: X ~ HS (μ, σ), де:

• X - це випадкова величина;
• μ - параметр зсуву (-∞ ≤ μ ≤ + ∞);
  
• σ - масштабний параметр (0 <σ).
  

Допустимий діапазон випадкової величини X: -∞ ≤ X ≤ + ∞.

Наведемо його наступним чином за допомогою класу CHypersecdist:

class CHypersecdist {public: double mu, sig; void CHypersecdist () {mu = 0,0; sig = 1.0; if (sig <= 0.) Alert ( "bad sig in Hyperbolic Secant Distribution!"); } Double pdf (double x) {return sech ((M_PI * (x-mu)) / (2 * sig)) / 2 * sig; } Double cdf (double x) {return 2 / M_PI * atan (exp ((M_PI * (x-mu) / (2 * sig)))); } Double invcdf (double p) {if (! (P> 0. && p <1.)) Alert ( "bad p in Hyperbolic Secant Distribution!"); return (mu + (2.0 * sig / M_PI * log (tan (M_PI /2.0 * p)))); } Double sf (double x) {return 1 -cdf (x); }};

Неважко помітити, що цей розподіл отримало свою назву від функції гіперболічного секанса, якого пропорційна першому.

Функція гіперболічного секанса sech виглядає так:

// + ----------------------------------------------- ------------------- + // | Hyperbolic Secant Function | // + ----------------------------------------------- ------------------- + double sech (double x) {return 2 / (pow (M_E, x) + pow (M_E, -x)); }

2.1.5 Р аспределеніе Стьюдента

Важливим розподілом в статистиці є розподіл Стьюдента .

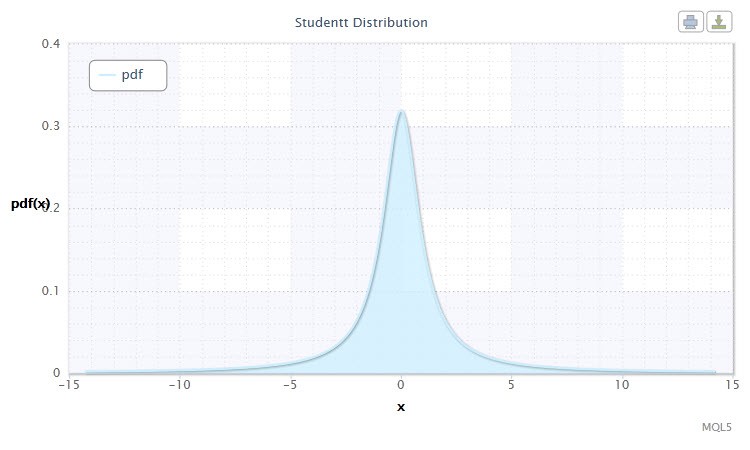
Малюнок 5. Щільність розподілу Стьюдента Stt (1,0,1)

Воно має наступну нотацію: t ~ Stt (ν, μ, σ), де:

• t - це випадкова величина, обрана з розподілу Стьюдента Stt;
• ν - це параметр форми (ν> 0)
  
• μ - параметр зсуву (-∞ ≤ μ ≤ + ∞);
  
• σ - масштабний параметр (0 <σ).
  

Допустимий діапазон випадкової величини X: -∞ ≤ X ≤ + ∞.

Часто, особливо при тестуванні гіпотез, використовується стандартизоване розподіл Стьюдента , З параметрами μ = 0 і σ = 1. Таким чином, воно перетворюється в однопараметричне розподіл з параметром ν.

Цей розподіл використовують при оцінюванні математичного очікування, прогнозного значення і інших характеристик за допомогою довірчих інтервалів, по перевірці гіпотез про значення математичних очікувань, коефіцієнтів регресійної залежності, гіпотез однорідності вибірок і т.д.

Уявімо його класом CStudenttdist:

class CStudenttdist: CBeta {public: int nu; double mu, sig, np, fac; void CStudenttdist () {int Nu = 1; double Mu = 0.0, Sig = 1.0; setCStudenttdist (Nu, Mu, Sig); } Void setCStudenttdist (int Nu, double Mu, double Sig) {nu = Nu; mu = Mu; sig = Sig; if (sig <= 0. || nu <= 0.) Alert ( "bad sig, nu in Student-t Distribution!"); np = 0.5 * (nu + 1.); fac = gammln (np) -gammln (0.5 * nu); } Double pdf (double x) {return exp (-np * log (1. + Pow ((x-mu) / sig, 2.) / Nu) + fac) / (sqrt (M_PI * nu) * sig); } Double cdf (double t) {double p = 0.5 * betai (0.5 * nu, 0.5, nu / (nu + pow ((t-mu) / sig, 2))); if (t> = mu) return 1.-p; else return p; } Double invcdf (double p) {if (p <= 0. || p> = 1.) Alert ( "bad p in Student-t Distribution!"); double x = invbetai (2. * fmin (p, 1.-p), 0.5 * nu, 0.5); x = sig * sqrt (nu * (1.-x) / x); return (p> = 0.5? mu + x: mu-x); } Double sf (double x) {return 1 -cdf (x); } Double aa (double t) {if (t <0.) Alert ( "bad t in Student-t Distribution!"); return 1.-betai (0.5 * nu, 0.5, nu / (nu + pow (t, 2.))); } Double invaa (double p) {if (! (P> = 0. && p <1.)) Alert ( "bad p in Student-t Distribution!"); double x = invbetai (1.-p, 0.5 * nu, 0.5); return sqrt (nu * (1.-x) / x); }};

З лістингу класу CStudenttdist слід, що для нього базовим класом є CBeta, який описує неповну бета-функцію .

Клас CBeta представимо в такий спосіб:

class CBeta: public CGauleg18 {private: int Switch; double Eps, Fpmin; public: void CBeta () {int swi = 3000; setCBeta (swi, EPS, FPMIN); }; void setCBeta (int swi, double eps, double fpmin) {Switch = swi; Eps = eps; Fpmin = fpmin; }; double betai (const double a, const double b, const double x); double betacf (const double a, const double b, const double x); double betaiapprox (double a, double b, double x); double invbetai (double p, double a, double b); };

У класу так само є свій базовий клас CGauleg18, який надає коефіцієнти для такого методу чисельного інтегрування, як квадратура Гаусса - Лежандра .

2.1.6 Логістичне р аспределеніе

Наступним для вивчення розподілом пропоную вважати логістичне .

Малюнок 6. Щільність логістичного р аспределенія Logi (0,1)

Воно має наступну нотацію: X ~ Logi (α, β), де:

• X - це випадкова величина;
• α - параметр зсуву (-∞ ≤ α ≤ + ∞);
  
• β - масштабний параметр (0 <β).
  

Допустимий діапазон випадкової величини X: -∞ ≤ X ≤ + ∞.

Клас CLogisticdist є реалізацією описаного розподілу:

class CLogisticdist {public: double alph, bet; void CLogisticdist () {alph = 0,0; bet = 1.0; if (bet <= 0.) Alert ( "bad bet in Logistic Distribution!"); } Double pdf (double x) {return exp (- (x-alph) / bet) / (bet * pow (1. + Exp (- (x-alph) / bet), 2)); } Double cdf (double x) {double et = exp (- 1. * fabs (1.81379936423421785 * (x-alph) / bet)); if (x> = alph) return 1 ./ (1. + et); else return et / (1. + et); } Double invcdf (double p) {if (p <= 0. || p> = 1.) Alert ( "bad p in Logistic Distribution!"); return alph + 0.551328895421792049 * bet * log (p / (1.-p)); } Double sf (double x) {return 1 -cdf (x); }};

2.1.7 Експоненціальне р аспределеніе

Давайте також подивимося на експоненціальне розподіл випадкової величини.

Малюнок 7. Щільність експоненціального р аспределенія Exp (1)

Воно має наступну нотацію: X ~ Exp (λ), де:

• X - це випадкова величина;
• λ - (λ> 0).
  

Допустимий діапазон випадкової величини X: 0 ≤ X ≤ + ∞.

Цей розподіл цікаво тим, що описує послідовність подій, що відбуваються одне за іншим в якісь моменти часу. Так, за допомогою цього розподілу трейдер може аналізувати збиткову серію угод та ін.

У MQL5 коді розподіл оформлено класом CExpondist:

class CExpondist {public: double lambda; void CExpondist () {lambda = 1.0; if (lambda <= 0.) Alert ( "bad lambda in Exponential Distribution!"); } Double pdf (double x) {if (x <0.) Alert ( "bad x in Exponential Distribution!"); return lambda * exp (-lambda * x); } Double cdf (double x) {if (x <0.) Alert ( "bad x in Exponential Distribution!"); return 1 .- exp (-lambda * x); } Double invcdf (double p) {if (p <0. || p> = 1.) Alert ( "bad p in Exponential Distribution!"); return - log (1.-p) / lambda; } Double sf (double x) {return 1 -cdf (x); }};

2.1.8 Гамма-р аспределеніе

Наступним видом безперервного розподілу випадкової величини я обрав гамма-розподіл .

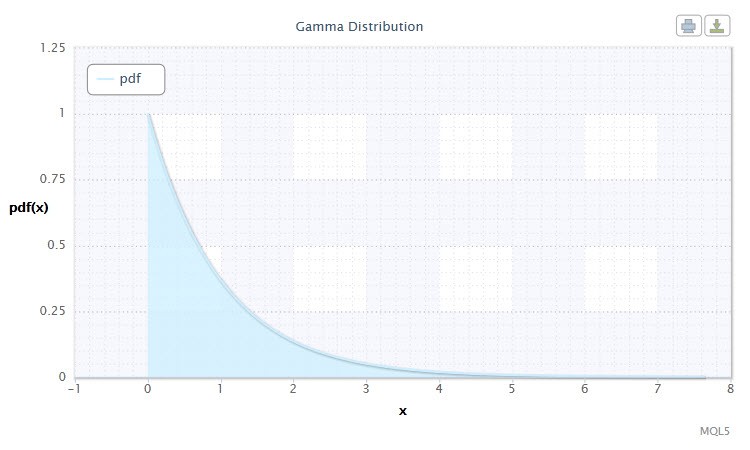
Малюнок 8. Щільність гамма р аспределенія Gam (1,1).

Його нотація виглядає наступним чином: X ~ Gam (α, β), де:

• X - це випадкова величина;
• α - параметр форми (0 <α);
  
• β - масштабний параметр (0 <β).
  

Допустимий діапазон випадкової величини X: 0 ≤ X ≤ + ∞.

У класовому варіанті CGammadist воно представлено так:

class CGammadist: CGamma {public: double alph, bet, fac; void CGammadist () {setCGammadist (); } Void setCGammadist (double Alph = 1.0, double Bet = 1.0) {alph = Alph; bet = Bet; if (alph <= 0. || bet <= 0.) Alert ( "bad alph, bet in Gamma Distribution!"); fac = alph * log (bet) -gammln (alph); } Double pdf (double x) {if (x <= 0.) Alert ( "bad x in Gamma Distribution!"); return exp (-bet * x + (alph- 1.) * log (x) + fac); } Double cdf (double x) {if (x <0.) Alert ( "bad x in Gamma Distribution!"); return gammp (alph, bet * x); } Double invcdf (double p) {if (p <0. || p> = 1.) Alert ( "bad p in Gamma Distribution!"); return invgammp (p, alph) / bet; } Double sf (double x) {return 1 -cdf (x); }};

Клас гамма-розподілу є похідним від класу CGamma, який, який описує неповну гамма-функцію .

Клас CGamma представимо в такий спосіб:

class CGamma: public CGauleg18 {private: int ASWITCH; double Eps, Fpmin, gln; public: void CGamma () {int aswi = 100; setCGamma (aswi, EPS, FPMIN); }; void setCGamma (int aswi, double eps, double fpmin) {ASWITCH = aswi; Eps = eps; Fpmin = fpmin; }; double gammp (const double a, const double x); double gammq (const double a, const double x); void gser (double & gamser, double a, double x, double & gln); double gcf (const double a, const double x); double gammpapprox (double a, double x, int psig); double invgammp (double p, double a); };

Клас CGamma, як і клас CBeta, має базовим класом клас CGauleg18.

2.1.9 Бета-р аспределеніе

Ну і давайте також представимо бета-розподіл .

Малюнок 9. Щільність бета- р аспределенія Beta (0.5, 0.5)

Його нотація виглядає наступним чином: X ~ Beta (α, β), де:

• X - це випадкова величина;
• α - 1-ий параметр форми (0 <α);
  
• β - 2-ий параметр форми (0 <β).
  

Допустимий діапазон випадкової величини X: 0 ≤ X ≤ 1.

Клас CBetadist характеризує цей розподіл так:

class CBetadist: CBeta {public: double alph, bet, fac; void CBetadist () {setCBetadist (); } Void setCBetadist (double Alph = 0.5, double Bet = 0.5) {alph = Alph; bet = Bet; if (alph <= 0. || bet <= 0.) Alert ( "bad alph, bet in Beta Distribution!"); fac = gammln (alph + bet) -gammln (alph) -gammln (bet); } Double pdf (double x) {if (x <= 0. || x> = 1.) Alert ( "bad x in Beta Distribution!"); return exp ((alph- 1.) * log (x) + (bet- 1.) * log (1.-x) + fac); } Double cdf (double x) {if (x <0. || x> 1.) Alert ( "bad x in Beta Distribution"); return betai (alph, bet, x); } Double invcdf (double p) {if (p <0. || p> 1.) Alert ( "bad p in Beta Distribution!"); return invbetai (p, alph, bet); } Double sf (double x) {return 1 -cdf (x); }};

2.1.10 Р аспределеніе Лапласа

Ще одним цікавим безперервним розподілом є розподіл Лапласа (Подвійне експоненціальне).

Малюнок 10. Щільність р аспределенія Лапласа Lap (0, 1)

Воно має таку нотацію: X ~ Lap (α, β), де:

• X - це випадкова величина;
• α - параметр зсуву (-∞ ≤ α ≤ + ∞);
• β - параметр масштабу (0 <β).

Допустимий діапазон випадкової величини X: -∞ ≤ X ≤ + ∞.

Клас CLaplacedist для розподілу представимо так:

class CLaplacedist {public: double alph; double bet; void CLaplacedist () {alph =. 0; bet = 1 .; if (bet <= 0.) Alert ( "bad bet in Laplace Distribution!"); } Double pdf (double x) {return exp (- fabs ((x-alph) / bet)) / 2 * bet; } Double cdf (double x) {double temp; if (x <0) temp = 0.5 * exp (- fabs ((x-alph) / bet)); else temp = 1.- 0.5 * exp (- fabs ((x-alph) / bet)); return temp; } Double invcdf (double p) {double temp; if (p <0. || p> = 1.) Alert ( "bad p in Laplace Distribution!"); if (p <0.5) temp = bet * log (2 * p) + alph; else temp = - 1. * (bet * log (2 * (1.-p)) + alph); return temp; } Double sf (double x) {return 1 -cdf (x); }};

Отже, ми створили за допомогою MQL5 коду 10 класів для десяти безперервних розподілів. Крім цього, були створені ще класи, які, можна сказати, з'явилися додатковими, тому що виникала необхідність в специфічних функціях і методах (наприклад, CBeta і CGamma).

Тепер я пропоную зайнятися дискретними розподілами і створити кілька класів для цієї категорії розподілів.

2.2.1 Біноміальний розподіл

Давайте почнемо з біноміального розподілу .

Малюнок 11. Щільність біноміального р аспределенія Bin (100, 0.5).

Його нотація виглядає наступним чином: k ~ Bin (n, p), де:

• k - це випадкова величина;
• n - число випробувань (0 ≤ n);
• p - ймовірність успіху (0 ≤ p ≤1).

Допустимий діапазон випадкової величини X: 0 або 1.

Чи не наводить вас на думку діапазон можливих значень випадкової величини X? Адже сукупність виграшних (1) і програшних угод (0) торгової системи теж можна аналізувати за допомогою цього розподілу.

Створимо клас СBinomialdist наступним чином:

class CBinomialdist: CBeta {public: int n; double pe, fac; void CBinomialdist () {setCBinomialdist (); } Void setCBinomialdist (int N = 100, double Pe = 0.5) {n = N; pe = Pe; if (n <= 0 || pe <= 0. || pe> = 1.) Alert ( "bad args in Binomial Distribution!"); fac = gammln (n + 1.); } Double pdf (int k) {if (k <0) Alert ( "bad k in Binomial Distribution!"); if (k> n) return 0.; return exp (k * log (pe) + (nk) * log (1.-pe) + fac-gammln (k + 1.) - gammln (nk + 1.)); } Double cdf (int k) {if (k <0) Alert ( "bad k in Binomial Distribution!"); if (k == 0) return 0.; if (k> n) return 1.; return 1.-betai ((double) k, n-k + 1., pe); } Int invcdf (double p) {int k, kl, ku, inc = 1; if (p <= 0. || p> = 1.) Alert ( "bad p in Binomial Distribution!"); k = fmax (0, fmin (n, (int) (n * pe))); if (p <cdf (k)) {do {k = fmax (k-inc, 0); inc * = 2; } While (p <cdf (k)); kl = k; ku = k + inc / 2; } Else {do ​​{k = fmin (k + inc, n + 1); inc * = 2; } While (p> cdf (k)); ku = k; kl = k-inc / 2; } While (ku-kl> 1) {k = (kl + ku) / 2; if (p <cdf (k)) ku = k; else kl = k; } Return kl; } Double sf (int k) {return 1.-Cdf (k); }};

2.2.2 Розподіл Пуассона

наступним стане розподіл Пуассона .

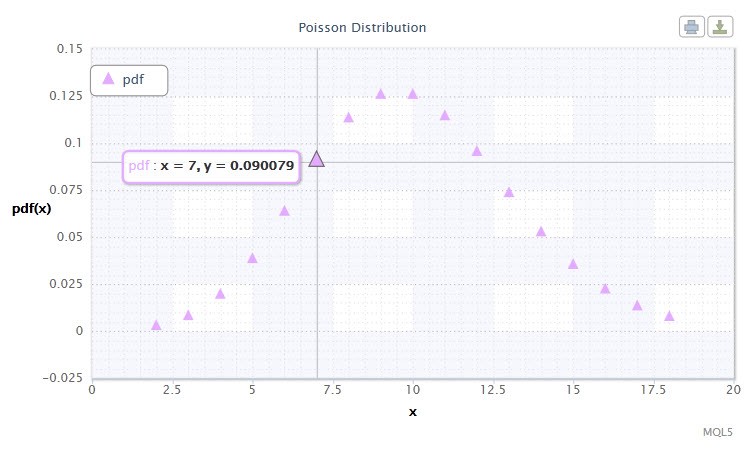
Малюнок 12. Щільність р аспределенія Пуассона Pois (10).

Його нотація виглядає наступним чином: k ~ Pois (λ), де:

• k - це Випадкове величина;
• λ - параметр положення (0 <λ).

Допустимий діапазон випадкової величини X: 0 ≤ X ≤ + ∞.

Розподіл Пуассона описує "закон рідкісних подій", що є важливим моментом при визначенні ступеня ризику.

Класом для розподілу послужить CPoissondist:

class CPoissondist: CGamma {public: double lambda; void CPoissondist () {lambda = 15.; if (lambda <= 0.) Alert ( "bad lambda in Poisson Distribution!"); } Double pdf (int n) {if (n <0) Alert ( "bad n in Poisson Distribution!"); return exp (-lambda + n * log (lambda) -gammln (n + 1.)); } Double cdf (int n) {if (n <0) Alert ( "bad n in Poisson Distribution!"); if (n == 0) return 0.; return gammq ((double) n, lambda); } Int invcdf (double p) {int n, nl, nu, inc = 1; if (p <= 0. || p> = 1.) Alert ( "bad p in Poisson Distribution!"); if (p <exp (-lambda)) return 0; n = (int) fmax (sqrt (lambda), 5.); if (p <cdf (n)) {do {n = fmax (n-inc, 0); inc * = 2; } While (p <cdf (n)); nl = n; nu = n + inc / 2; } Else {do ​​{n + = inc; inc * = 2; } While (p> cdf (n)); nu = n; nl = n-inc / 2; } While (nu-nl> 1) {n = (nl + nu) / 2; if (p <cdf (n)) nu = n; else nl = n; } Return nl; } Double sf (int n) {return 1.-Cdf (n); }};

Природно, в рамках однієї статті неможливо розглянути всі статистичні розподілу, та й напевно, в цьому немає необхідності. За бажанням користувач може розширити представлену галерею розподілів. Створені розподілу знаходяться в файлі Distribution_class.mqh.

3. Створення графіків розподілів

Тепер пропоную подивитися, як ми можемо використовувати для подальшої роботи наші створені для розподілів класи.

Тут я знову звернувся до ООП і написав клас CDistributionFigure, який обробляє розподілу певних користувачем параметрів і виводить його на екран засобами, описаними в статті "Графіки і діаграми в форматі HTML" .

class CDistributionFigure {private: Dist_type type; Dist_mode mode; double x; double x11; double x12; int d; double st; public: double xAr []; double p1 []; void CDistributionFigure (); void setDistribution (Dist_type Type, Dist_mode Mode, double X11, double X12, double St); void calculateDistribution (double nn, double mm, double ss); void filesave (); };

Реалізацію пропускаю. Зазначу, що в класі є такі члени-дані, як type і mode, що відносяться до типів Dist_type і Dist_mode відповідно. Ці типи є перерахуваннями досліджуваних розподілів і їх видів.

Отже, спробуємо нарешті створити графік якогось розподілу.

Для безперервних розподілів я написав скрипт continuousDistribution.mq5, основні рядки якого виглядають так:

input Dist_type dist; input Dist_mode distM; input int nn = 1; input double mm = 0., ss = 1 .; void OnStart () {double Xx1, // лівий межа Xx2, // правий межа st = 0.05; // крок if (dist == 0) {Xx1 = mm- 5.0 * ss / 1.25; Xx2 = mm + 5.0 * ss / 1.25; } If (dist == 2 || dist == 4 || dist == 5) {Xx1 = mm- 5.0 * ss / 0.35; Xx2 = mm + 5.0 * ss / 0.35; } Else if (dist == 1 || dist == 6 || dist == 7) {Xx1 = 0.001; Xx2 = 7.75; } Else if (dist == 8) {Xx1 = 0.0001; Xx2 = 0.9999; st = 0.001; } Else {Xx1 = mm- 5.0 * ss; Xx2 = mm + 5.0 * ss; } CDistributionFigure F; // створення екземпляра класу CDistributionFigure F.setDistribution (dist, distM, Xx1, Xx2, st); F.calculateDistribution (nn, mm, ss); F.filesave (); string path = TerminalInfoString (TERMINAL_DATA_PATH) + "\\ MQL5 \\ Files \\ Distribution_function.htm"; ShellExecuteW (NULL, "open", path, NULL, NULL, 1); }

Для дискретних розподілів написаний скрипт discreteDistribution.mq5.

Я запустив скрипт зі стандартними параметрами для розподілу Cauchy і отримав наступний графік, представлений на ролику нижче.

Висновок

У статті були представлені і закодовані в форматі MQL5 деякі теоретичні розподілу випадкової величини. Вважаю, що сама ринкова торгівля, а значить, і робота торгової системи повинна бути заснована на фундаментальних імовірнісних законах.

Сподіваюся, що стаття принесе практичну користь для зацікавлених читачів. Я, зі свого боку, збираюсь розвинути цю тему і на практичних прикладах продемонструвати, яким чином можна використовувати статистичні розподілу ймовірностей при аналізі імовірнісних моделей.

Розташування файлів:

#
файл
шлях
описание
1
Distribution_class.mqh
% MetaTrader% \ MQL5 \ Include Галерея класів розподілів
2 DistributionFigure_class.mqh
% MetaTrader% \ MQL5 \ Include
Класи графічного відображення розподілів
3 continuousDistribution.mq5% MetaTrader% \ MQL5 \ Scripts Скрипт для створення безперервного розподілу
4
discreteDistribution.mq5
% MetaTrader% \ MQL5 \ Scripts Скрипт для створення дискретного розподілу
5
dataDist.txt
% MetaTrader% \ MQL5 \ Files Дані для відображення розподілу
6
Distribution_function.htm
% MetaTrader% \ MQL5 \ Files HTML-графік безперервного розподілу
7 Distribution_function_discr.htm
% MetaTrader% \ MQL5 \ Files HTML-графік дискретного розподілу
8 exporting.js
% MetaTrader% \ MQL5 \ Files Java-скрипт для експорту графіка
9 highcharts.js
% MetaTrader% \ MQL5 \ Files JavaScript-бібліотека 10 jquery.min.js% MetaTrader% \ MQL5 \ Files JavaScript-бібліотека

література:

1. K. Krishnamoorthy. Handbook of Statistical Distributions with Applications , Chapman and Hall / CRC 2006.
   
2. WH Press, et al. Numerical Recipes: The Art of Scientific Computing , Third Edition, Cambridge University Press: 2007. - тисячу двісті п'ятьдесят шість pp.
   
3. Булашев С.В. Статистика для трейдерів . - М .: Компанія Супутник +, 2003. - 245 с.
4. Гайдишев І. Аналіз і обробка даних: спеціальний довідник - СПб: Пітер, 2001. - 752 с .: іл.
5. Кібзун А.І., Горяїнова О.Р. - Теорія ймовірностей і математична статистика. Базовий курс з прикладами і завданнями
6. Кремер Н.Ш. Теорія ймовірностей і математична статистика М .: Юніті-Дана, 2004. - 573 с.