Наше деловое партнерство www.banwar.org

З е ток м е тод, збірна назва групи наближених методів вирішення диференціальних, інтегральних і інтегро-диференціальних рівнянь. Стосовно до диференціальних рівнянь з приватними похідними термін «З. м. »використовується як синонім термінів« метод кінцевих різниць »і« різницевий метод ». З, м. - один з найбільш поширених наближених методів вирішення завдань, пов'язаних з диференціальнимирівняннями. Широке застосування С. м. Пояснюється його великою універсальністю і порівняльною простотою реалізації на ЕОМ.

Суть С. м. Полягає в наступному: область безперервної зміни аргументів, в якій шукається рішення рівняння, доповненого, якщо необхідно, крайовими і початковими умовами, замінюється дискретним безліччю точок (вузлів), званим сіткою; замість функцій неперервного аргументу розглядаються функції дискретного аргументу, що визначаються в вузлах сітки і звані сітковими функціями; похідні, що входять в рівняння, крайові та початкові умови, апроксимуються різницевими відносинами; інтеграли аппроксимируются квадратурними формулами; при цьому вихідне рівняння (завдання) замінюється системою (лінійних, якщо вихідна задача була лінійної) алгебраїчних рівнянь (системою сіткових рівнянь, а стосовно до диференціальних рівнянь - різницевої схемою).

Якщо отримана таким чином система сіткових рівнянь можна вирішити, принаймні, на досить дрібній сітці, т. Е. Сітці з густим розташуванням вузлів, і її рішення при необмеженому здрібнінні сітки наближається (сходиться) до вирішення вихідного рівняння (завдання), то отримане на будь-якій фіксованій сітці рішення і приймається за наближене рішення вихідного рівняння (завдання).

для одновимірного теплопровідності рівняння

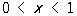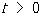, , , (1)

з початковим u (х, 0) = u0 (x) і крайовим умовами u (0, t) = m 1 (t), u (1, t) = m 2 (t) [передбачається, що u0 (0) = m 1 (0), u0 (1) = m 2 (0)] на прямокутної рівномірної сітці з вузлами (xi = ih, tj = jt), де i = 0, 1, 2, ..., N, j = 0, 1, 2, ..., h = 1 / N і t> 0 - кроки сітки, найбільш часто використовувана різницева схема виглядає так (схема з вагами):

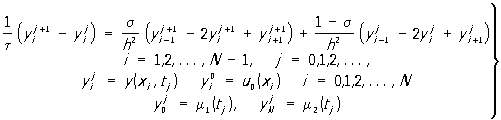(2)

де s - деякий параметр. для двовимірного Пуассона рівняння

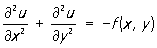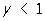,, , (3)

з однорідними крайовими умовами u (0, у) = u (х, 0) = u (1, у) = u (х, 1) = 0 на прямокутної рівномірної сітці з вузлами xi1 = i1h1, yi2 = i2h2, де i1 = 0, 1, ..., N1, i2 = 0, 1, ..., N2, h1 = 1 / N1, h2 = 1 / N2, найбільш вживаною є різницева схема:

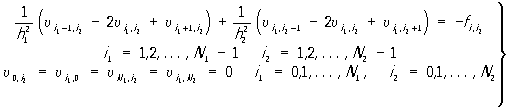(4)

для інтегрального рівняння

,

,

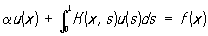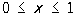на рівномірній сітці з вузлами xi = ih, де i = 0, 1, 2, ..., N, h = 1 / N, найпростіша система сіткових рівнянні має вигляд:

,

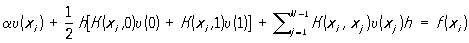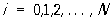
Крім зазначених вище рівномірних прямокутних сіток, можуть використовуватися сітки загальнішого вигляду, наприклад нерівномірні, а для рівняння (3) і непрямокутні. Сіткові рівняння на таких сітках виглядають більш складно. Якщо рівняння (3) вирішується в області, відмінною від прямокутника, то навіть на рівномірній прямокутній сітці апроксимація крайових умов стає менш очевидною.

При виборі тієї чи іншої сіткової апроксимації велике значення має величина похибки апроксимації (п. А.). Так, для рівнянь (2) п. А. є величина O (t + h2) при будь-якому s, O (t2 + h2) при s = 0.5 і O (t2 + h 4) при s = 0,5 - h2 / 12 t. Для схеми (4) п. А. є величина O (h12 + h22). Наявність гарної апроксимації рівнянь і крайових умов сітковими рівняннями ще не гарантує того, що рішення системи сіткових рівнянь буде в певному сенсі близько до вирішення вихідної задачі. Потрібно ще, щоб рішення сіткових рівнянь було стійким, т. Е. Безперервно (рівномірно безперервно щодо вибору сітки) залежало від правої частини і початкових і крайових даних. Тільки наявність гарної апроксимації і стійкості гарантує збіжність рішень сіткових рівнянь до вирішення вихідного рівняння при необмеженому здрібнінні сітки. Відзначимо, що схема (2) стійка при 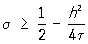; при s = 0 виходить явна схема, стійка за умови .

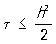Системи сіткових рівнянь є системи лінійних алгебраїчних рівнянь. Порядок системи буде тим вище, чим дрібніше сітка. Але точність наближеного рішення залежить від величини кроків сітки, і вона тим більше, чим менше кроки. Тому що виходять алгебри зазвичай мають досить високий порядок.

Літ .: Самарський А. А., Введення в теорію різницевих схем, М., 1971; Годунов С. К., Рябенький В. С., Різницеві схеми, М., 1973.

В. Б. Андрєєв, А. А. Самарський.